Heap

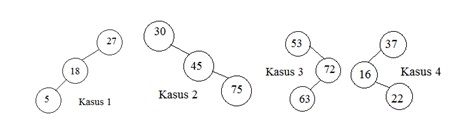
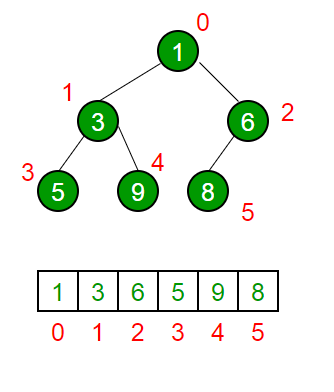
-> Heap adalah struktur data yang berbentuk complete binary tree dan menggunakan array dalam mengimplementasikannya.

-> Terdapat 3 jenis heap yang dapat kita pelajari

-> Min Heap

Pada jenis min heap ini, root node pada tree akan menyimpan value atau angka terkecil sedangkan node-node child yang akan dimiliki oleh root tersebut, akan lebih besar valuenya.



-> Max Heap

Pada jenis max heap ini, root node pada tree akan menyimpan value atau angka terbesar sedangkan node-node child yang akan dimiliki oleh root tersebut, akan lebih kecil valuenya.





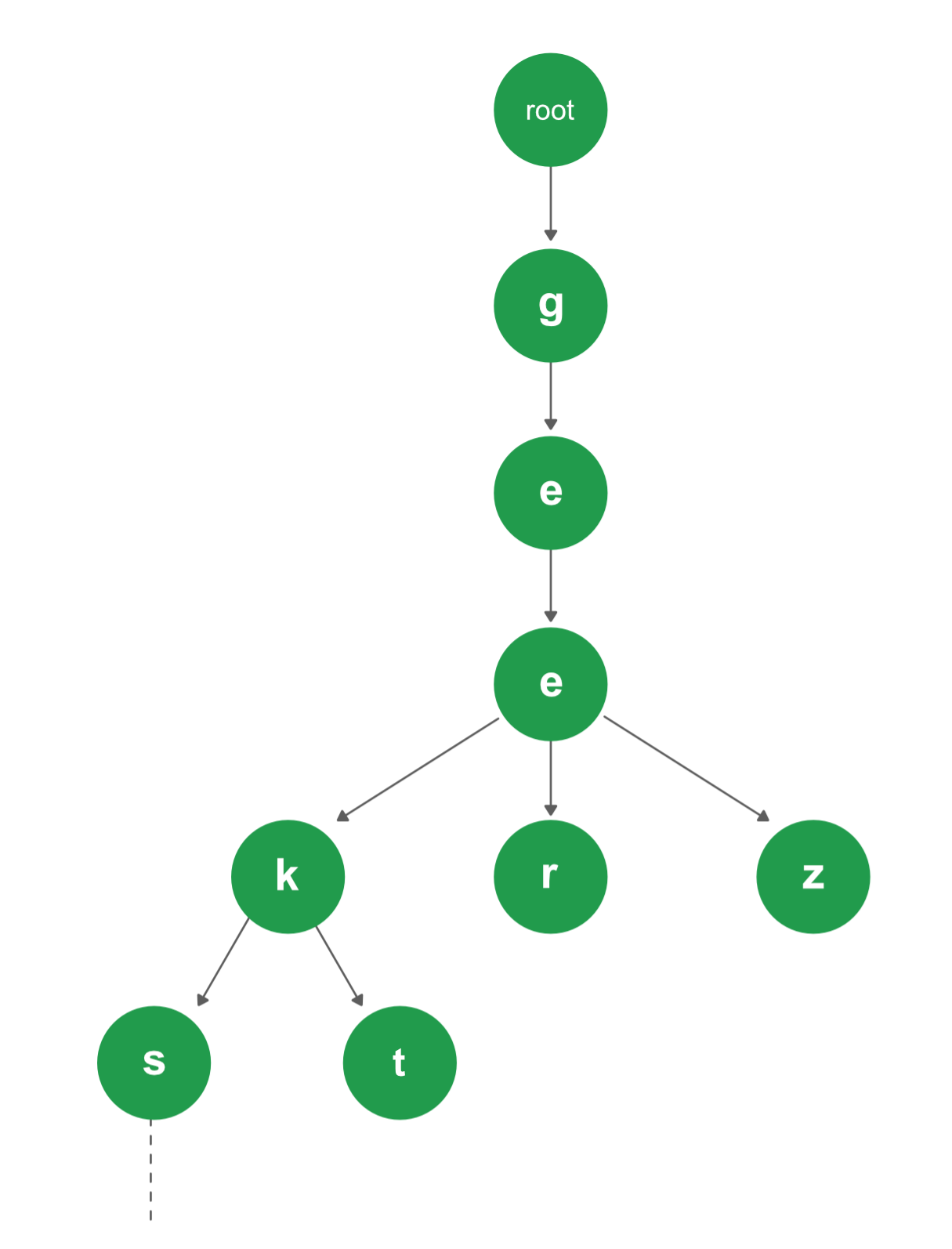
-> Trie

Trie adalah struktur data berupa pohon terurut untuk menyimpan suatu himpunan string dimana setiap node pada pohon tersebut mengandung awalan (prefix) yang sama, karena itulah trie disebut juga pohon prefix. Tujuan trie ini adalah untuk menyimpan string ataupun pencarian string mejadi lebih cepat dan mengurangi kompleksitas yang ada.






Reference :
https://www.geeksforgeeks.org/binary-heap/
https://www.geeksforgeeks.org/max-heap-in-java/
https://informatika.stei.itb.ac.id/~rinaldi.munir/Matdis/2010-2011/Makalah2010/MakalahStrukdis2010-091.pdf

AVL TREE

AVL TREE

AVL Tree merupakan turunan tree ataupun struktur tree yang lebih baik dibandingkan BST. Kenapa lebih baik? Dikarenakan konsep yang dimiliki oleh AVL Tree membuatnya memiliki struktur tree yang balance sehingga untuk melakukan pencarian data pun akan lebih cepat dan lebih mudah dibandingkan Binary Search Tree.

Ada 4 kondisi yang biasanya terjadi saat operasi insert dilakukan, yaitu :
anggap T adalah node yang harus diseimbangkan kembali
– kondisi 1 : node terdalam terletak pada subtree kiri dari anak kiri T (left-left)
– kondisi 2 : node terdalam terletak pada subtree kanan dari anak kanan T (right-right)
– kondisi 3 : node terdalam terletak pada subtree kanan dari anak kiri T (right-left)
– kondisi 4 : node terdalam terletak pada subtree kiri dari anak kanan T (left-right)







https://socs.binus.ac.id/2016/12/20/insertion-avl-tree/
https://www.geeksforgeeks.org/avl-tree-set-1-insertion/